Improved Generative Adversarial Network - Youtube

WGAN - 影片0:57

• Wasserstein Distance (Earth Mover's Distance)
• Weight Clipping

Earth Mover's Distance

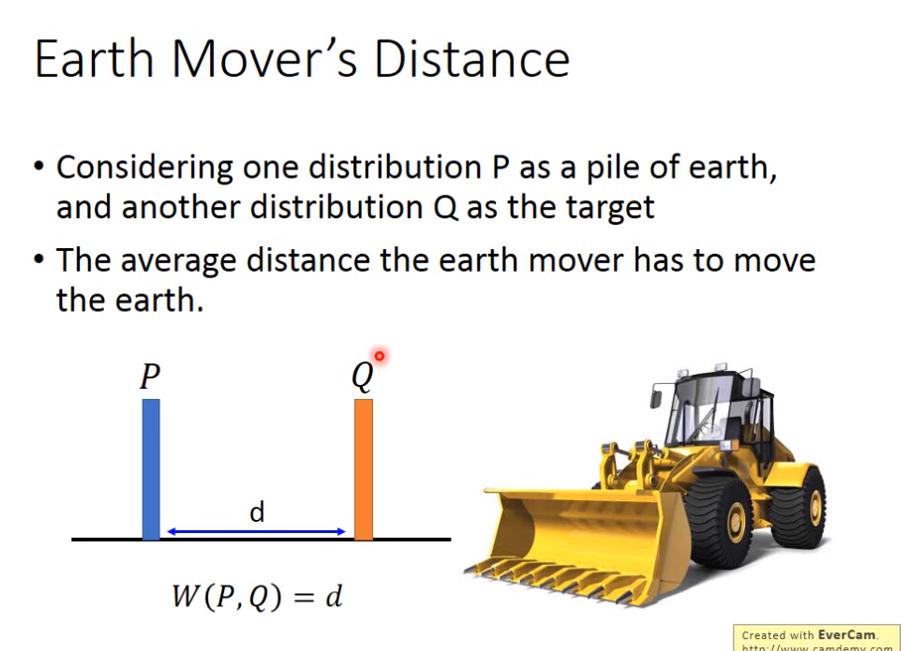
• earth mover 原意為推土機
• Earth Mover's Distance 可以看作是 推土機平均要把土運送多遠

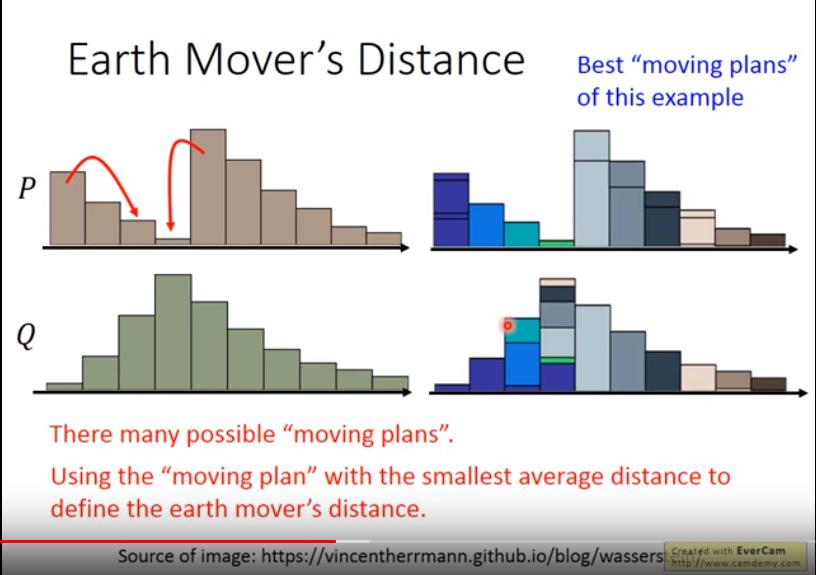
• 但是要把 P 推土成 Q，可能有非常多種規劃，我們選的是 average distance 最小的規劃，將其 average distance 作為 Earth Mover's Distance

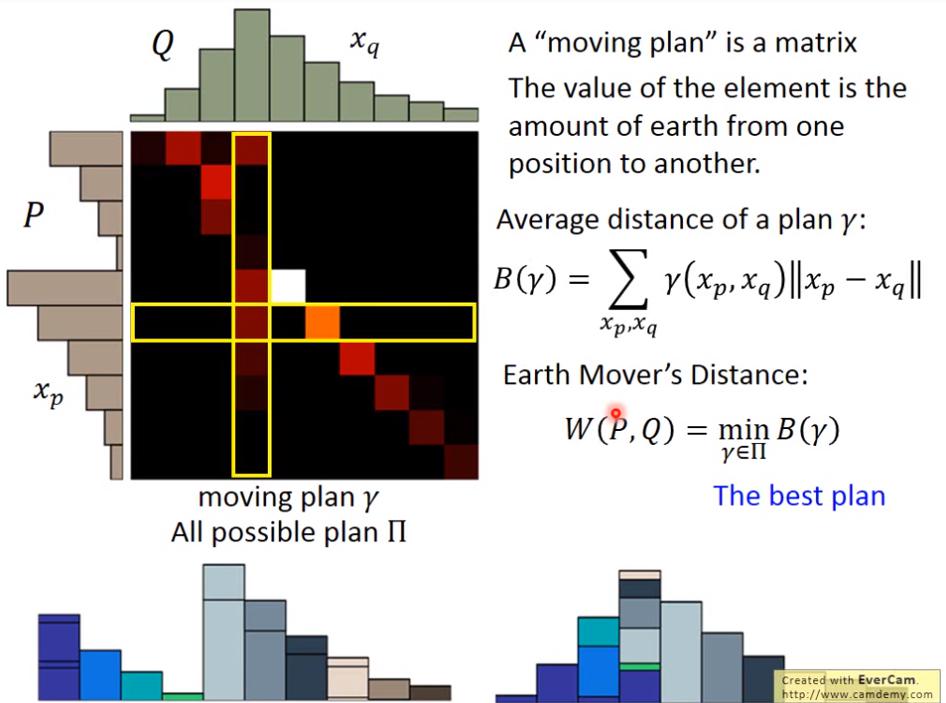我覺得矩陣的意義有點像 confusion matrix 或 transition matrix吧

Average distance of a plan $\gamma$：$B(\gamma)=\sum_\limits{x_p,x_q} \gamma(x_p,x_q)||x_p-x_q||$

• $x_p,x_q$：P和Q的機率分布(點?)
• $\gamma (x_p,x_q)$：從 $x_p$ 運送到 $x_q$ 的量

Wasserstein Distance：$W(P,Q)=\min_\limits{r\in \Pi}B(\gamma)$

總之 Distance 不是 f-divergence，但是可以寫成下面這個形式： $W(P_{data},P_G)=\max_\limits{D\in 1-Lipschitz} \{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[f^*(D(x))]\}$

• 也就是說我們希望找到一個 D，若 x 屬於 data 的分布，可以最大化D(x)的期望值；若 x 屬於 G 的分布，可以最小化 D(x) 的期望值。
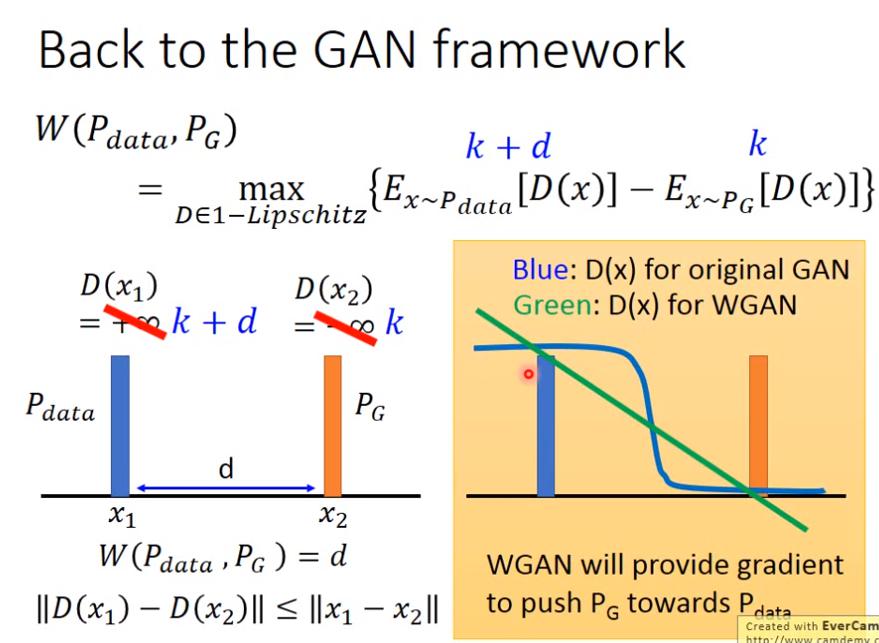
  • 但是這樣一來，只要讓$D(x_{data})$ 是無窮大、$D(x_G)$ 是負無窮大，那就好啦，但是這樣做並不make sense，而且實務上會遇到一些麻煩，所以我們需要對 D 作一些限制，也就是 1-Lipschitz 的限制

那麼要怎麼作到 K-Lipschitz 的 constraint 呢?

• Weight Clipping

• 若 D 的 weight 是一條直線、data 的 distribution 是藍bar、G 的 distribution 是橘 bar，則
  • 若不作 weight clipping，直線斜率會越 train 越接近無窮大。

小結：Algorithm of original GAN & WGAN

原始GAN的部分可以回頭看 這

WGAN 與原始 GAN 的差異

D 與原始 GAN 的差異

• V 去掉 log
• D 的 output 不取 sigmoid (也是因為去掉log了，就不需要讓 output 在0~1之間)
• weight clipping

G 與原始 GAN 的差異

• minimize 的對象改成 $- \frac{1}{m} \sum_{i=1}^m D(G(z^i))$

都市傳說

• 不能用 Adam，要用 RMSprop
  • 但是在 improved WGAN 裡面又發現 Adam 比較好

D的 loss 大，代表 generate 的東西不好；反之則好 應該是指D(G)吧

Improved WGAN

• 一個可微函數是 1-Lipschitz的 若且唯若 它的 gradient 在任何地方都不大於1
  • $D\in \text{1-Lipschitz}\longleftrightarrow ||\nabla D(x)|| \leq 1 \ ,\forall x$

不可能對所有 x 作積分，因此從 $P_{penalty}$ 作 sampling

為什麼 $P_{penalty}$ 只要在 $P_{data}$ 和 $P_G$ 之間呢? 因為我們只在乎 G 能不能朝向 data 逼近

如果要滿足 1-Liptschitz 的條件，那 weight 的 norm 應該要小於 1 啊，可是為什麼 regularization term 卻要改成 $(||\nabla_x D(x)||-1)^2$，導致 $||\nabla_x D(x)||$ 越接近 1 越好呢? 其實 paper 的 Appendix 有證明，不過其實有一個比較直觀的想法可以參考：

• 因為我們不僅希望 $||\nabla_x D(x)||$ 小於1，還希望他盡量大，這樣 $D(x_{data})$ 會更大、$D(x_G)$ 會更小。

Sentence Generation (WGAN)