ML Lecture 20: Support Vector Machine

• 先以+1和-1表示兩個分類
  • $\hat y^1 ... \hat y^n$ 表示第一筆資料到第n筆資料的label，值為+1或-1
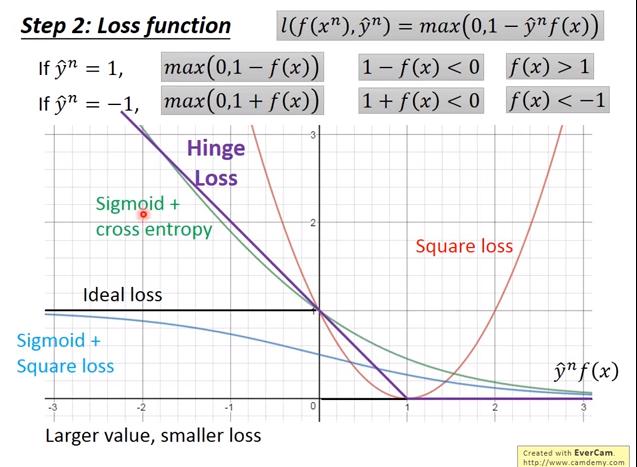
  • 我們期望 $\hat y^n$ 與 $f(x)$ 的乘積越大 越好，因此 $\hat y^n f(x)$ 越大，loss應該要越小
  • 理想狀況是：$\hat y^n f(x)$ 為正，則loss=0，$\hat y^n f(x)$為負，則loss=1，但是這個loss function無法微分，不能做gradient descent
  • hinge loss: 只要 $\hat y^n f(x)>1$ loss就是0，否則 $\hat y^n f(x)$ 越小，loss越大
    • hinge loss 比較不怕 outlier
    • 使用 hinge loss，當 $\hat y^n = 1$ 時，只要 $f(x)>1$，loss就是0；當 $\hat y^n = -1$ 時，只要 $f(x) < -1$，loss 就是0

Linear SVM

• hinge loss 是 convex function
• regularization term 也是 convex function
• 相加仍為 convex function，gradient descent做起來相當簡單

• 與 logistic regression 唯一的差別是 loss function ，使用 cross entropy 就是 LR，使用 hinge loss 就是 linear SVM

• 可以有deep structure

  • YiChuang Tang, "Deep Learning using Linear Support Vector Machines", ICML 2013

• 也可以使用 gradient descent 解

gradient descent

結論：$\dfrac{\partial L(f)}{\partial w_i} = \sum_n -\delta(\hat y^nf(x^n) < 1)\hat y^nx_i^n$

• depends on 參數 $w$，$-\delta(\hat y^nf(x^n) < 1)\hat y^n$ 可以用 $c^n(w)$ 來代替

Linear SVM - another formulation (我們熟悉的 SVM 樣貌)

注意上圖兩個紅框框裡面的式子代表不一樣的意義

• 但是因為 loss function 要 minimize $\epsilon^n$，下面的紅色框就和上面的紅色框相同了

損失函數 $L(f) = \sum_\limits{n}{l(f(x^n),\hat y^n)}+\lambda ||w||_2$

• $l(f(x^n),\hat y^n)$ : hinge loss，即 $max(0,1-\hat y^nf(x^n))$
• $\lambda ||w||_2$: regularization項

現在把 hinge loss 換成 $\epsilon^n$，即

• $\epsilon^n = max(0,1-\hat y^nf(x^n))$
• $L(f) = \sum_\limits{n}{\epsilon^n}+\lambda ||w||_2$

而我們想 minimize loss 的時候，$\epsilon^n = max(0,1-\hat y^nf(x))$ 這件事等同於

• $\epsilon^n \geq 0$
• $\epsilon^n \geq 1-\hat y^nf(x)$ 即 $\hat y^nf(x) \geq 1-\epsilon^n$

也就是說當我們無法達到 $\hat y^nf(x) \geq 1$ 時，$\epsilon^n$ 可以放寬我們的標準(根據2式)，故 $\epsilon^n$又名 slack variable

Dual Representation

而最後解出來的 w 可以視為 data point 的 linear combination，即
$w^* = \sum_\limits n \alpha_n^*x^n$
WHY?
一般會使用 Lagrange Multiplier 解出之前提到的式子來證明，不過現在用 gradient descent 的觀點來看這件事
Gradient Descent 對於第i維的w，update

• $w_i \leftarrow w_i - \eta \sum_\limits n c^n(w)x_i^n$
  • $c^n(w) = \frac{\partial l(f(x^n,\hat y^n))}{\partial f(x^n)} = -\delta(\hat y^nf(x^n)<1)\hat y^n$

也就是 $w \leftarrow w - \eta \sum_\limits n c^n(w)x^n$

以 hinge loss 而言，大多數的 $c^n(w)$ 會等於0，也就是 $w^* = \sum_\limits n \alpha_n^*x^n$ 中大多數的 $\alpha_n^*$ 會等於0，只有幾個 data point 的係數不為0，而係數不為0的那些 $x^n$ ，就被稱為 support vector。 若w初始化為0，則最後得到的w會是 data point 的 linear combination。而使用 data point 的 linear combination 做為w的好處是，可以使用到 kernel method

kernel method

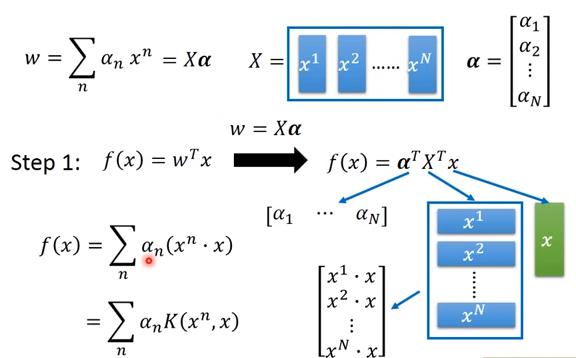$w = X\alpha$， 所以 $f(x) =w^Tx = \alpha^TX^Tx = \sum_\limits n \alpha_n(x^n\cdot x)$ 我們又可以把 $x^n\cdot x$ 寫成 $K(x^n,x)$ 因此 $f(x) = \sum_\limits n \alpha_nK(x^n,x)$ $f(x)$ 中，只有$\alpha$是未知的，也就是說我們的目的是找出$[\alpha_1,\alpha_2, ... ,\alpha_n]$使得 loss function 最小

因此我們只需要知道 $K(x, z)$ 是多少，並不需要知道 $x$ 這個 vector 是長什麼樣子

Kernel Trick

當我們要把所有的 $x$ transform 成 $\phi(x)$ 時，kernel trick 很有用 Q: $K(x, z)$ 的定義就是兩個 vector 做完 feature transform $\phi$ 之後的內積 $\phi(x)\cdot\phi(z)$ 嗎???

舉例 1

• $x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$
• $\phi(x) = \begin{bmatrix} {x_1}^2 \\ \sqrt 2 x_1x_2 \\ {x_2}^2\end{bmatrix}$
• $K(x, z) = \phi(x)\cdot\phi(z) = \begin{bmatrix}{x_1}^2 \\ \sqrt 2 x_1x_2 \\ {x_2}^2\end{bmatrix}\cdot \begin{bmatrix}{z_1}^2 \\ \sqrt 2 z_1z_2 \\ {z_2}^2\end{bmatrix} = {x_1}^2{z_1}^2 + 2x_1x_2z_1z_2+{x_2}^2{z_2}^2$ 這是土法煉鋼的算法
• 我們可以把上面那個 $K(x, z)$ 的結果轉換成 $(x_1z_1+x_2z_2)^2 = (x\cdot z)^2$，這樣可以省下許多計算
  • 個人理解：假設 $x$ 為 $n_x$ 維的 vector；$\phi(x)$ 為 $n_\phi$ 維的 vector，則計算 $\phi(x)$ 和 $\phi(z)$ 都需要 $n_\phi$ 次計算、計算 $\phi(x)\cdot\phi(z)$ 需要 $n_\phi$ 次計算。因此一共至少要進行 $O(n_\phi)$ 次計算
  • 而直接計算 $(x\cdot z)^2$ 則只需要 $n_x$ 次計算

舉例 2

• 把 x 的部分串成一個 vector 就是 $\phi(x)$
• 把 z 的部分串成一個 vector 就是 $\phi(z)$

舉例 3 - Radial Basis Function Kernel

如果把 $\exp(-\frac{1}{2}||x-z||_2)$ 視為一個 kernel $K(x, z)$，則 feature transform 的維度會是無窮大，為什麼?

• $\exp(-\frac{1}{2}||x||_2)$ 只和 $x$ 有關，因此我們用 $C_x$ 表示它；同理，我們用 $C_z$ 來表示 $\exp(-\frac{1}{2}||z||_2)$
• 把 $C_xC_z\exp(x\cdot z)$ 用泰勒展開會得到後面那行的結果 (可以視為無窮多維的 feature inner product)

RBF kernel因為是投射到無窮多維，所以比較容易overfitting

舉例 4 - Sigmoid Kernel

Sigmoid kernel $K(x, z) = \tanh(x\cdot z)$ 就像是單層 hidden layer 的 NN，而 neuron 的數目相當於 support vector 的數目

自訂 kernel function

也可以自訂kernel function，用類似similarity方式定義

• 當 x 是 structured object，很難設計一個 $\phi(x)$，很適用 kernel function
• 而 是否可以視為兩個 feature transform 的 inner product 可以用 Mercer's theory 檢查。

Deep Learning 和 SVM 的異同