Generative Adversarial Network

Maximum Likelihood Estimation

• Given a data distribution $P_{data}(x)$
• We have a distribution $P_G(x;\theta)$
  • We want to find $\theta$ such that $P_G(x;\theta)$ close to $P_{data}(x)$
• Sample $\{x^1,x^2,...,x^m\}$ from $P_{data}(x)$
• We can compute $P_G(x^i;\theta)$
• Likelihood of generating the samples $L = \prod_\limits{i=1}^mP_G(x^i;\theta)$
• Find $\theta^\star$ maximize the likelihood

於是乎

註

• $arg \max_\theta \sum log P_G(x;\theta)$：從 資料中 sample 出一些 x，x被 $\theta$ 產生出來的 log likelihood
• $arg \max_\theta E_{x \sim P_{data}} log P_G(x;\theta)$：(我認為是)當 x 服從 data 的機率分布時，$\theta$ 產生 x 的 log likelihood

• 總之任務是變成了 minimize 兩個機率分布的 KL divergence

$P_G(x) = \int_z P_{prior}(z)I_{[G(z)=x]}dz$

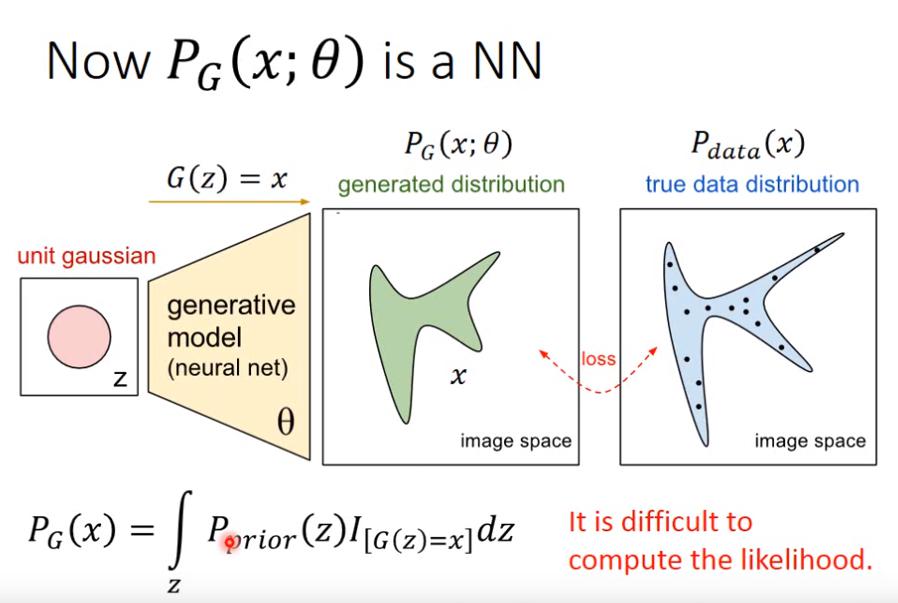
• $P_G(x)$：從 network 裡面 sample 出 x 的機率
• $P_{prior}(z)$：每個 z 出現的機率，若G(z)是NN則是每個 x 出現的機率?
• $I_{G(z)=x}$：每個 z 產生出的 G(z) 若和 x 相同，則 = 1，否則 = 0

問題是，likelihood 太難計算，因為 G(z) 非常複雜，要求出 x 的機率會很困難。那麼在無法知道 likelihood 的情況下，如何調整 $\theta$，使得 G(z) 的分布會和 data 的分布最接近呢? 這就是 GAN 的貢獻。

Basic Idea of GAN

接下來解釋 $G^* = ar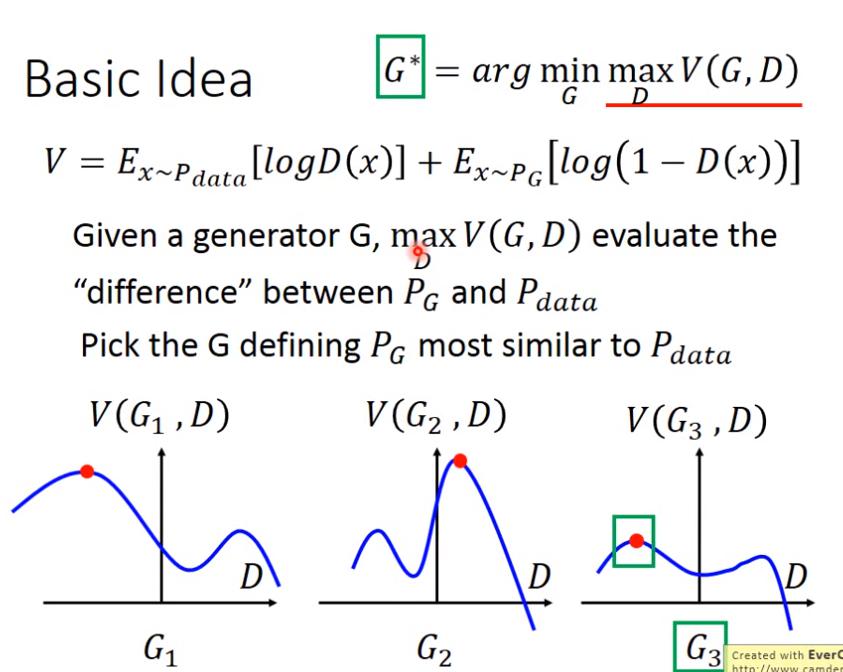g \min_\limits G \max_\limits D V(G,D)$ 的意義 圖中橫軸是D，縱軸是V(G,D)

• 給定G和D，則 $\max_\limits D V(G,D)$ 是座標中的紅點(曲線最高處)
  • 而且若 V定義為 $E_{x\sim P_{data}}[logD(x)] +E_{x\sim P_{G}}[log(1-D(x))]$，則 V(G,D)可以視為 Generator 和 data 之間的某種 divergence
  • 我認為就是，D要最大化D所計算出的 generator 和 data 之間的 divergence，G要最小化 D所得到的 divergence
• 假設G只有圖中三種，則 $arg \min_\limits G \max_\limits D V(G,D)$ 會選擇 $G_3$，因為紅點是三者中最低的

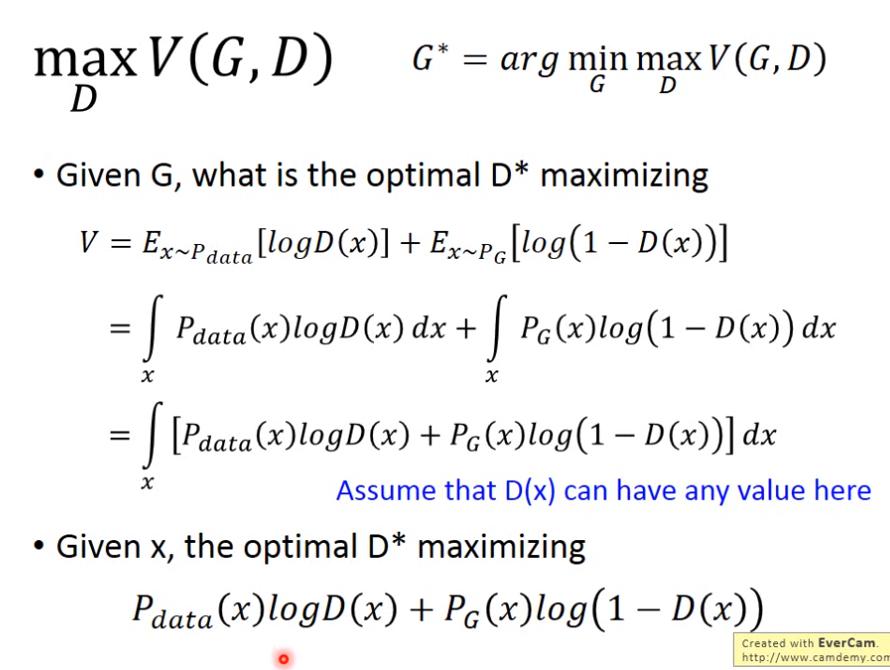總之最好的 D* 想要最大化 $\int_\limits{x} [P_{data}(x)logD(x)+P_G(X)log(1-D(x))] dx$ 也可以說是最大化 $P_{data}(x)logD(x)+P_G(X)log(1-D(x))$

總之 最好的 D，給定一筆資料 x 時， $D^*(x)=\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$ 這個式子就是在衡量 G 和 data 的某種 difference， 接下來說明 為什麼是在衡量 G和data的 difference呢

• 期望值可以視為積分
• 左式的 $log \frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$ 上下同乘 1/2，然後將上方的1/2提出來，會是 $\int_\limits x P_{data}(x)log\frac{1}{2} = log\frac{1}{2}$
  • 右式同理

於是公式就成了下面這樣

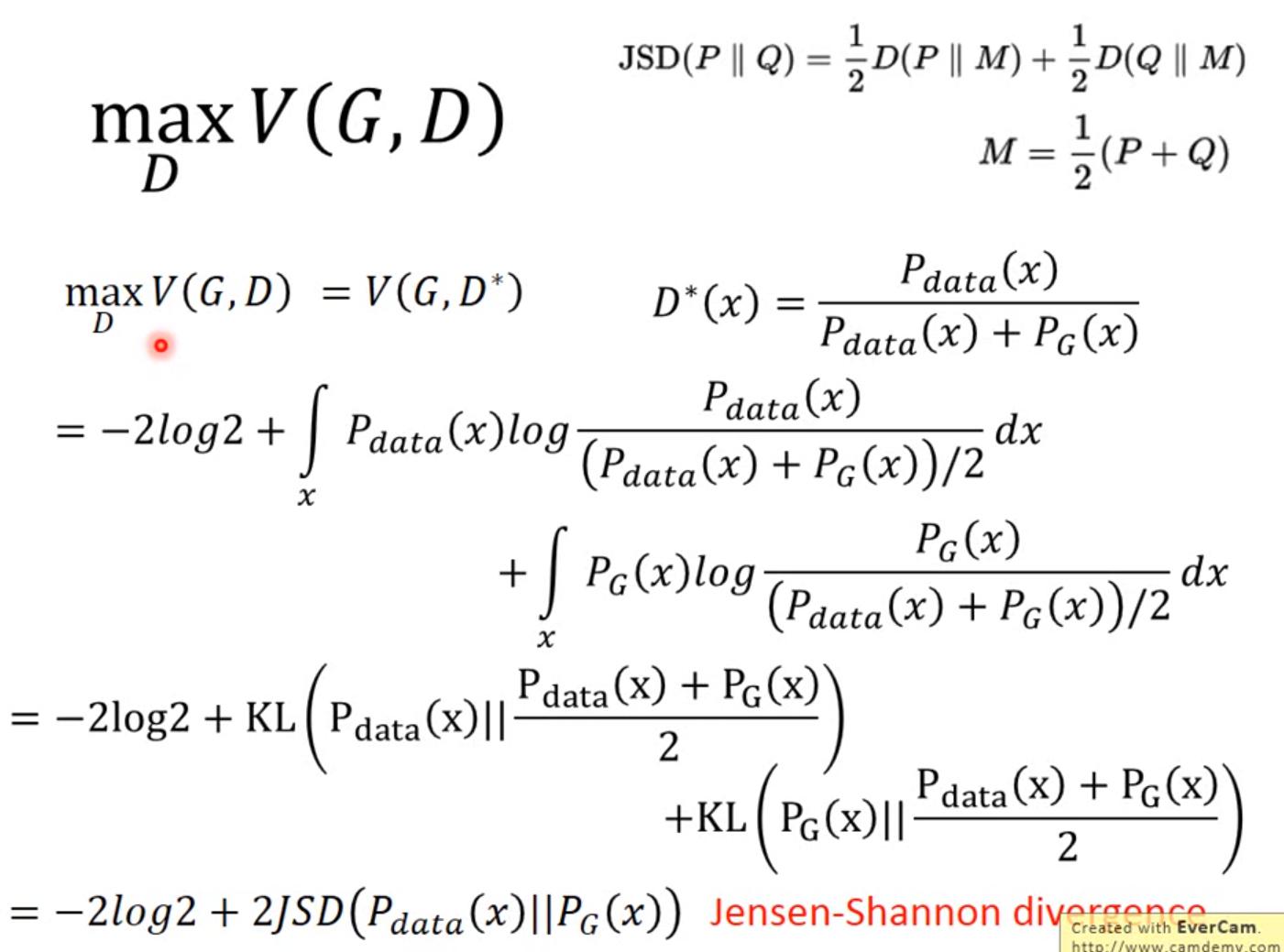
小結

兩個 distribution 若完全沒有任何交集，則 JS divergence = log 2，若完全一模一樣，則JS divergence = 0，也就是說 $\max_\limits D V(G,D)$ 最大值為0，最小值為 -2 log2

最好的 G 可以讓 $\max_\limits D V(G,D)$ 最小，此時 $P_G(x)=P_{data}(x)$

Algorithm

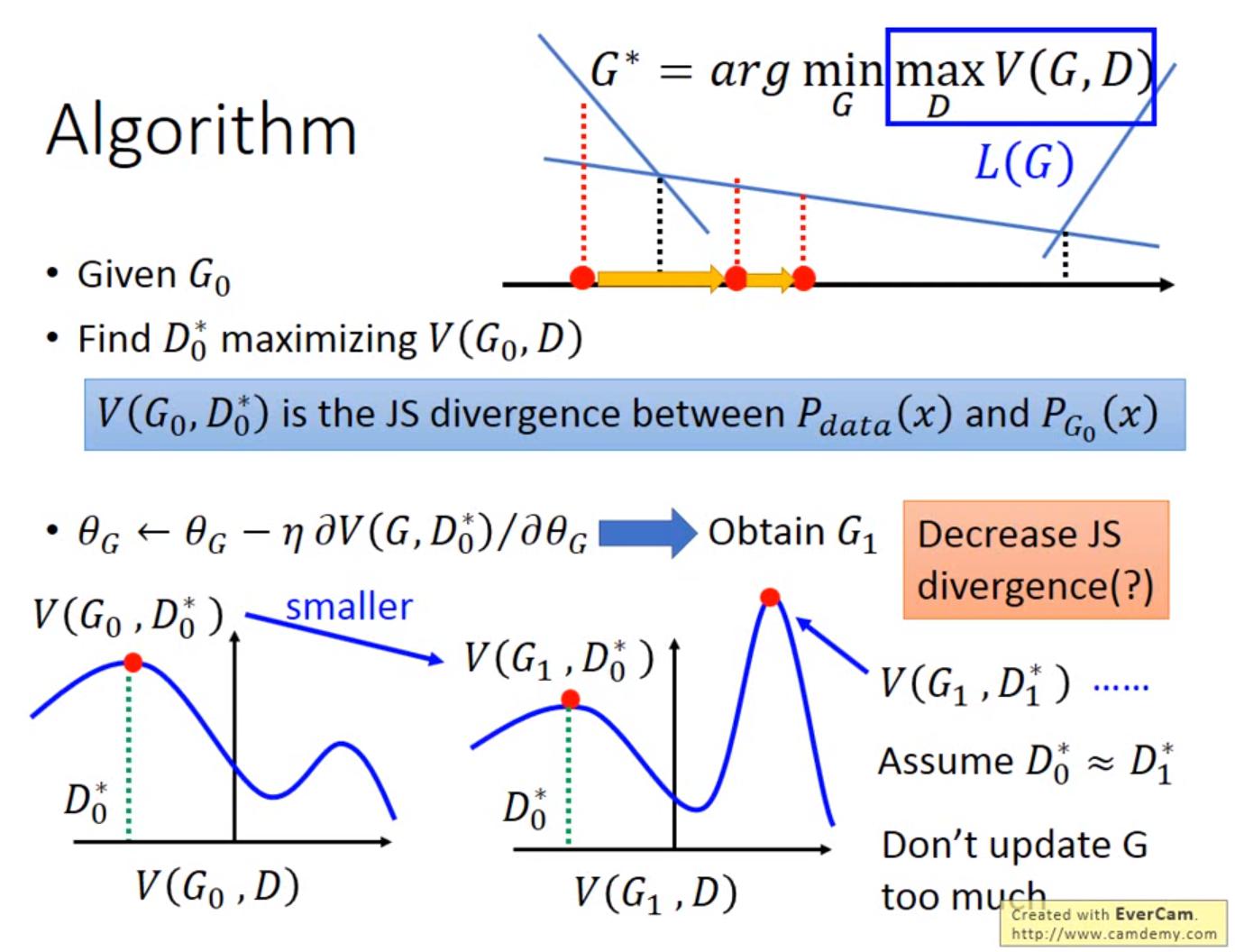
• G 不能 update 太多，因為這樣對該 Generator 來說 D* 會變很多，就不能保証新的 D 仍然是 $\max_\limits D V(G,D)$

定義 G的loss：$L(G) = arg \max_\limits D V(G,D)$

然後用 gradient descent 解 就出來了 耶結束了~~~(不是

In practice

• $\tilde V$ 是用來逼近 V 的。 此外，

Maximize $\tilde V = \frac{1}{m}\sum_\limits{i=1}^m log(D(x^i)) + \frac{1}{m}\sum_\limits{i=1}^m log(1-D(\tilde x^i))$

也可以視為 Minimize $L = -\frac{1}{m}\sum_\limits{i=1}^m log(D(x^i)) - \frac{1}{m}\sum_\limits{i=1}^m log(1-D(\tilde x^i))$

也就是 minimize cross entropy，亦即我們只要 train 一個 binary classifier 來分辨 G 和 data

• 在訓練 D 時，要訓練多次，因為要找到 maximum
  • 但 Ian Goodfellow 在 tutorial 說，他每個 iteration 訓練 D 也習慣只訓練一次
• 然而可能只找到 local optima，也就是說只能找到 $\max_\limits D V(G,D)$ 的 lower bound
• 訓練 G 時，只訓練一次，因為之前說過，G不能差太多
• 訓練 G 時，要 minimize $\tilde V$，但是左邊那一項和G無關，因此可以省略

承前面所述，理論上，G 應該要 minimize $V=E_{x\sim P_G}[log(1-D(x))]$ ，然而當D(G(z)) 很小的時候(即 G產生的樣本騙不過D)，此時梯度是很小的，因此訓練會變很慢。

解法是，將 objective function 改成 $V=E_{x\sim P_G}[-log(D(x))]$

• 一方面剛開始的訓練速度會變快，因梯度較大
• 另一方面，實作上的好處是，在這樣更新我們的 $P_G$ 時，等同於把$P_G$ 所產生的資料，當作是 discriminative 的 positive 的 example (???為啥)

這邊很玄哪 之後再看一次

因為D計算的是JSD，然而當兩個 distribution 沒有交集時，JSD都是 log2，因此G會沒有動力逼近 data distribution

一個解法是對 input data 或 label 增加 noise

Mode Collapse

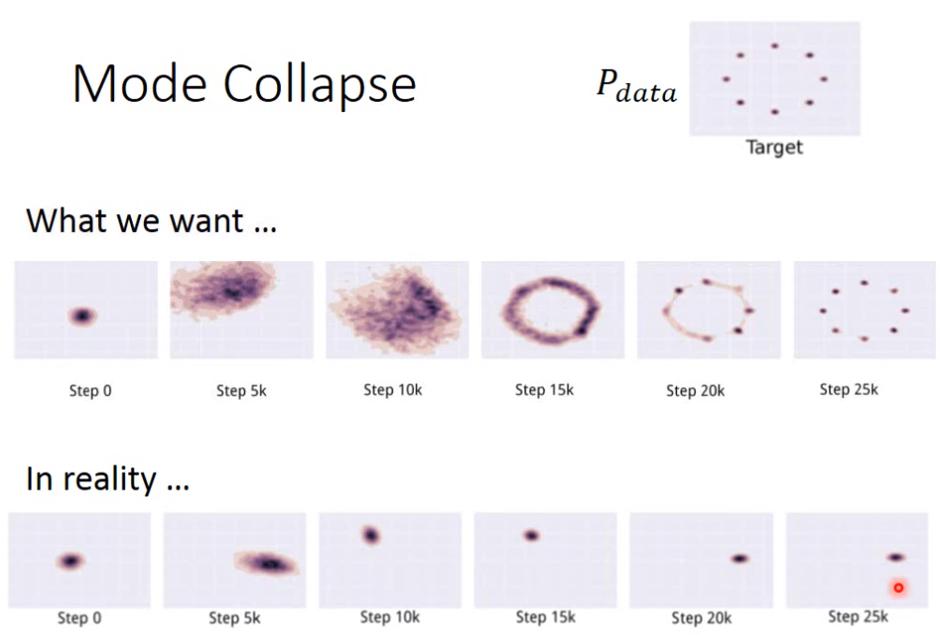
本來 Ian Goodfellow 以為發生 mode collapse 的原因是像下面這樣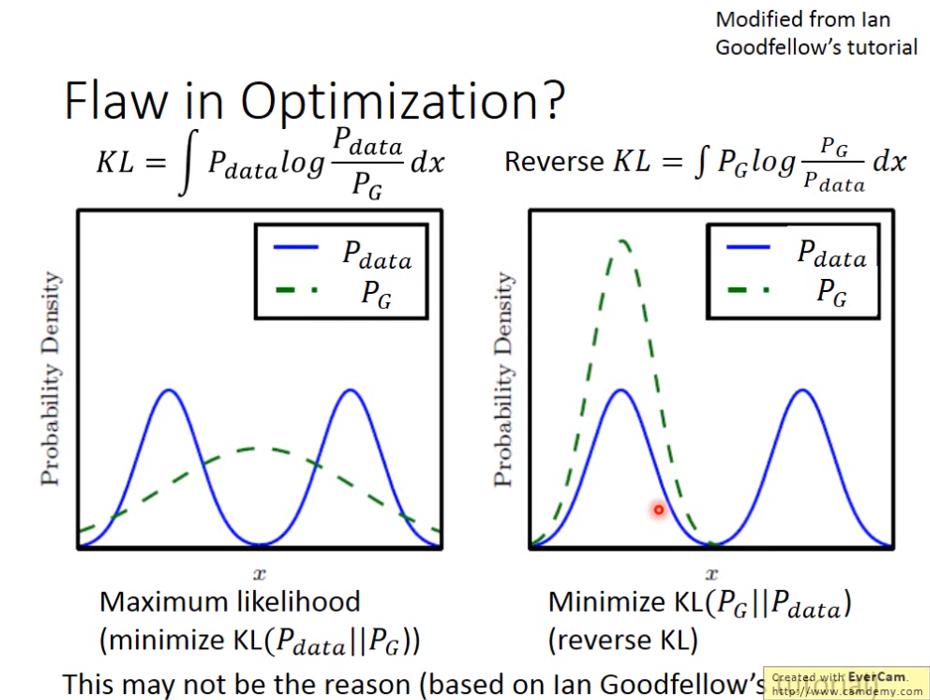： Ian Goodfellow 認為：如果今天 minimize 的是 KL divergence，則比較不容易發生 mode collapse，因為如果$P_{data}$ 可以產生 x 的地方，$P_G$ 不能產生 x 的話(即 $P_G = 0$)，則KL Divergence 會無窮大，因此在 minimize KL divergence 時，會將 $P_G$ 盡量涵蓋住所有 $P_{data}$ 的分布。 但是如果要 minimize 的是 Reverse KL divergence 的話，如果 $P_G$ 能產生 x 但是 $P_{data}$ 產生x的機率為0，則 reverse KL divergence 會是無窮大。那想 minimize 的話就會造成 $P_G$ 固守他找到的distribution，不敢去拓展新的distribution。

然而，我們如果直接 minimize KL divergence (藉由自己設定$V(G,D)$)，仍然會出現 mode collapse 的問題。

So many GANs

Conditional GAN

例如我們想 input text , output image 幹嘛不直接用NN做 supervised learning 就好了呢? 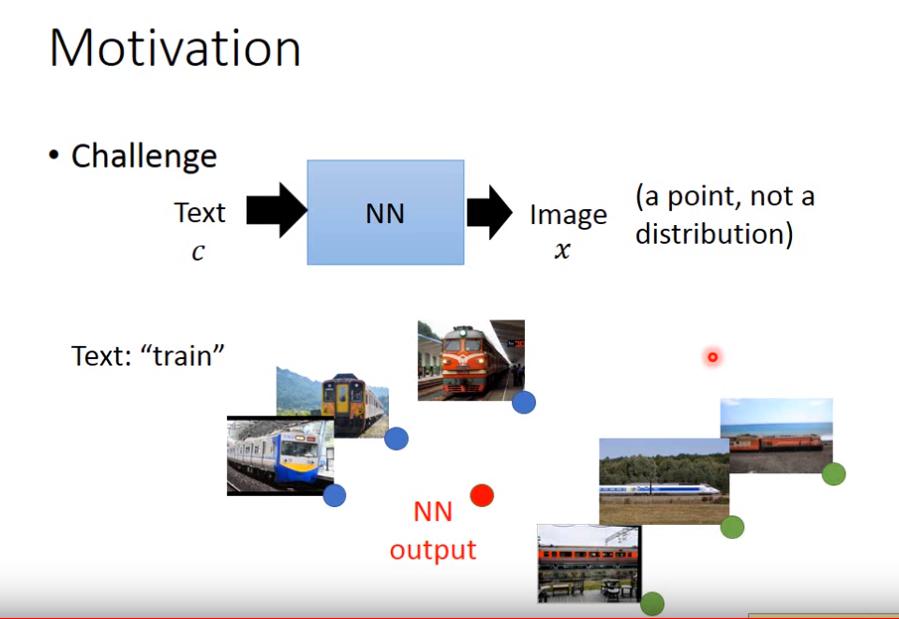一般的 supervised learning 只能對 data point 建模，因此 input "train"，他會 output 一張圖來 minimize 和所有火車圖片的誤差，那就會產生很模糊的圖片。

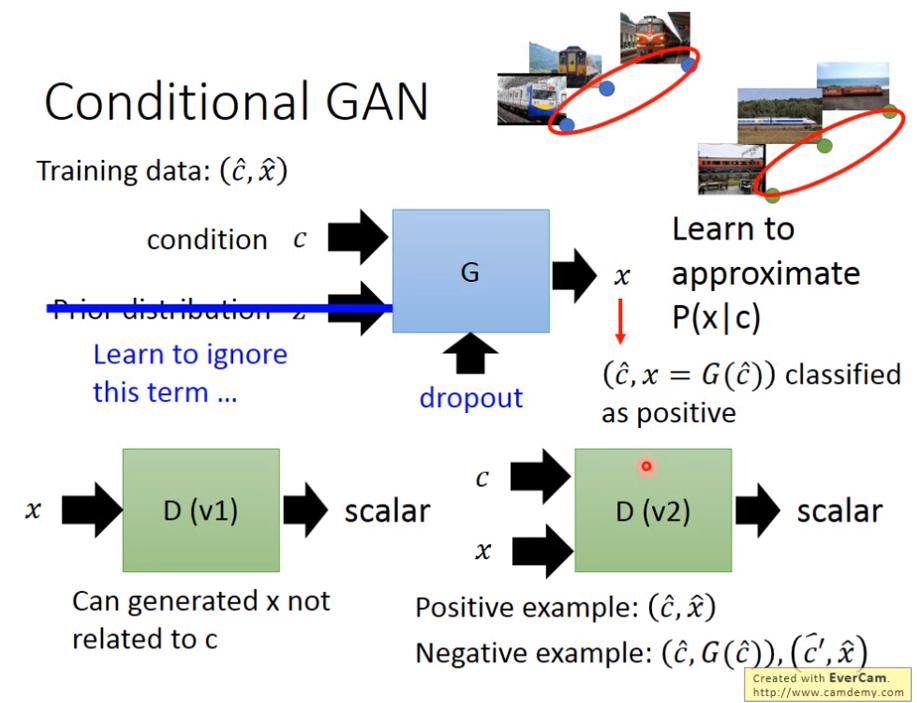
• GAN 和 NN 不一樣的是，GAN 可以學到資料的分布
• 然而做 conditional generation時，若 input c (類別) & z (noise)，有時候GAN也會無視z，直接根據c產生data，要解決這個問題可以將架構改成，不 input z 了，直接做dropout，這樣也可以有 random distribution 的效果。
• conditional GAN 的 discriminator 是 輸入c和x，輸出結果，positive 的資料是：正確的c和x對應， negative 的資料是：正確的c和generated data對應，以及不正確的c和真實資料對應；而 generator 想做的事情是：希望 正確的c和generatored資料的對應可以騙過 discriminator。