Video Here

Bagging

Review: Bias vs Variance

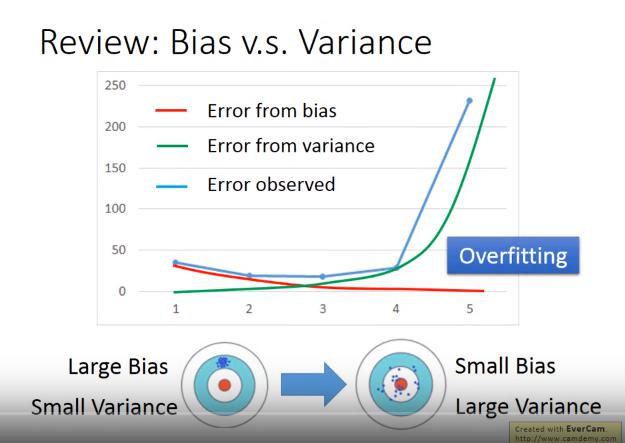
• Simple Model

  • large bias
  • small variance

• Complex Model

  • small bias
  • large variance

bagging

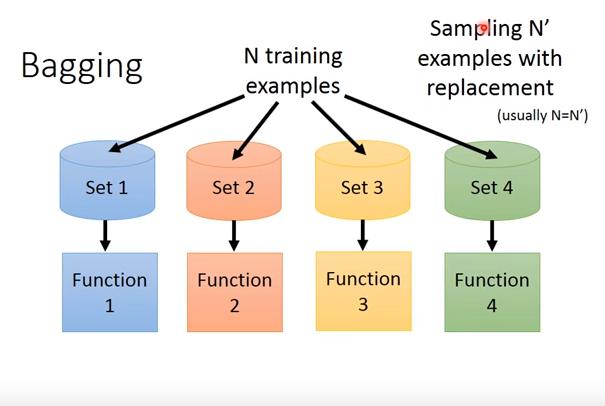
• 以N'筆資料(N'通常等於N, sampling with replacement)訓練不同的complex model，雖然每個model的variance大，但集合後可以有較小的variance，可以減少overfitting

• 因此當model很複雜、擔心它容易overfitting時，可以做bagging，例如

  • Decision Tree

• Random Forest

  • 用傳統的 bagging 的方法來做 decision tree 的 bagging 是不夠的，因為這樣會導致每棵樹都長得差不多
  • 根據 這篇 ，RandomForest 只能減少 variance，不能減少 bias，因此 base tree 的 bias 越小越好，也就是讓他 fully grow
  • Out-of-bag validation for bagging
    • 在做bagging的validation的時候(例如f1、f2做bagging)，只要使用他們都沒有用來train的資料當作validation data即可

Boosting

• 用來改善較弱的model (目標是降低training error嗎??)
• 保證
  • 若現有error rate<50% 的model
  • 則可以用來獲得 training error 0% 的model

Framework of Boosting

• 先取得一個分類器f1(x)
• 找到另一個f2(x)來幫助f1(x)，f2和f1盡量不同，才較有幫助
• 以此類推，結合各個classifier
• 分類器的訓練是有順序的

• $u^n$：第n筆資料的權重

Adaboost

• 找到一組training data使得f1(x)爆掉，再拿這組training data訓練出f2(x)
  • 找的方式其實是調整每個data的weight，使得f1(x)的錯誤率高達0.5，也就是放大答錯的data的weight
• $\epsilon_1$: 第一個 model $f_1$ 在第一次的 training data 上的 error rate
• $u_1^n$: 第 n 筆資料在 第一次 training data 上的權重
• $Z_1$: normalize 用的，第一次 training data 的權重加總
• $\frac{\sum_n u_2^n \delta(f_1(x^n)\neq \hat y^n)}{Z_2}$: 第一個 model 在第二次的 training data 上的 error rate
  • $\delta(f_1(x^n)\neq \hat y^n)$: 若預測值錯誤，則值為1，反之為0

• 答錯的 data，就將權重乘上 $d_1$，答錯的 data，將權重除以 $d_1$
• 找到 $d_1$ 使得 $f_1$ 錯誤率高達0.5

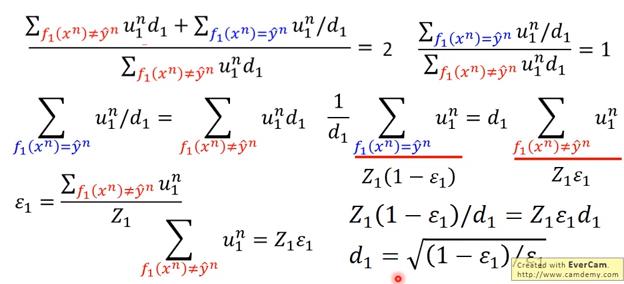
經過一番推導，可以得到 $d_1 = \sqrt{(1-\epsilon_1)/\epsilon_1}$

為何 Non-uniform weight 可以直接將 classifier 乘上 $\alpha_t$ ? 這段要重看

Adaboost 數學證明 (可以達到 0% error rate)

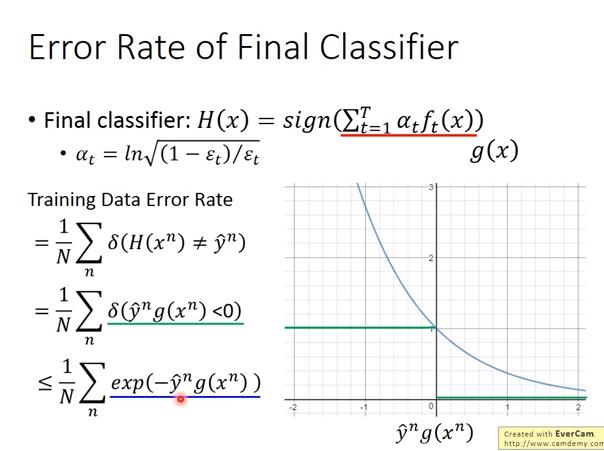
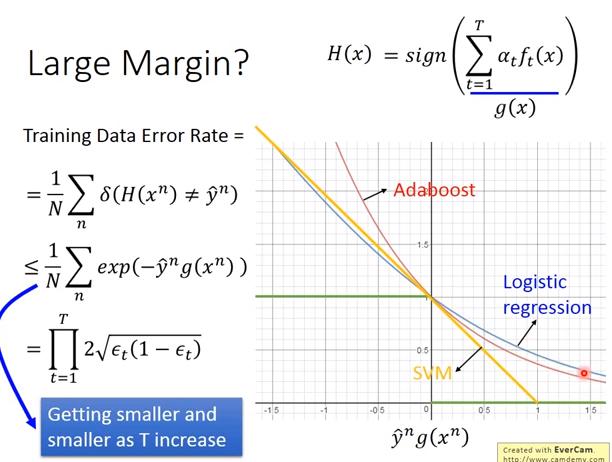
• $g(x)$ 現在代表每個時間 t 的 classifier 的 weighted sum
• Training data error rate 有一個 upper bound 是 $\frac{1}{N}\sum_\limits{n}exp(-\hat y^ng(x^n))$
• 現在要證明 這個 upper bound 可以越來越小

• $Z_{T+1} = \sum_\limits{n} exp(-\hat y^n \sum_\limits{t=1}^Tf_t(x^n)\alpha_t)$
• 又 $g(x) = \sum_\limits{t=1}^T\alpha_tf_t(x^n)$
• 因此 Training error 的 upper bound 就是 $\frac{1}{N} Z_{T+1}$

接下來要證明 $Z_T$，即 weight 的 summation 會越來越小

恩 證完了

Adaboost 特別處

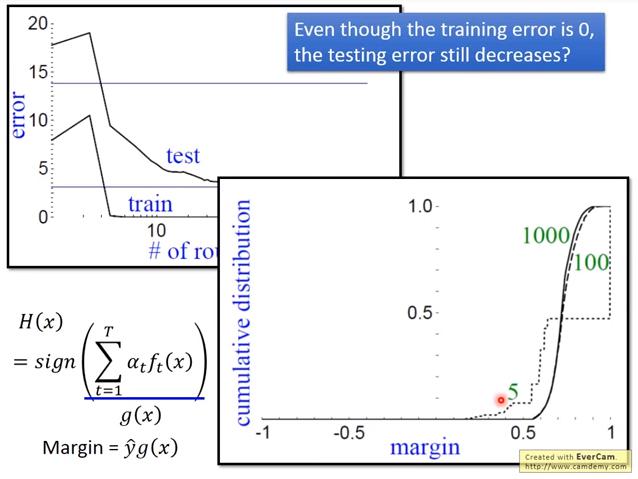
即使 training error rate 已經是 0，testing error 仍會繼續下降

Gradient Boosting

那 $\frac{\partial L(g)}{\partial g}$ 就等於 $\sum_\limits{n}exp(-\hat y^ng_{t-1}(x^n))(\hat y^n)$
而且我們希望 $f_t$ 和 $\frac{\partial L(g)}{\partial g}$ 的方向越相近越好

• $\alpha_t$ 就像 learning rate，但是以往 gradient 很好算，所以我們可以固定 learning rate，頂多多 train 幾次，但是現在好不容易找到一個 $f_t$ 所以要盡可能找到最好的 $\alpha_t$，來更新 $g$ 使得 Loss $L(g)$ 最小化。
• 結果發現找到的 $\alpha_t$ 和 adaboost 找到的一樣，但現在 Gradient Boosting 可以定義任何的 objective function。

Random Forest 和 Boosting 比較 (自己查的)

根據 這篇

• 當 feature 很多 (超過4000)，RandomForest 取得的表現通常較好，而4000以下，boosting似乎較佳。

Stacking

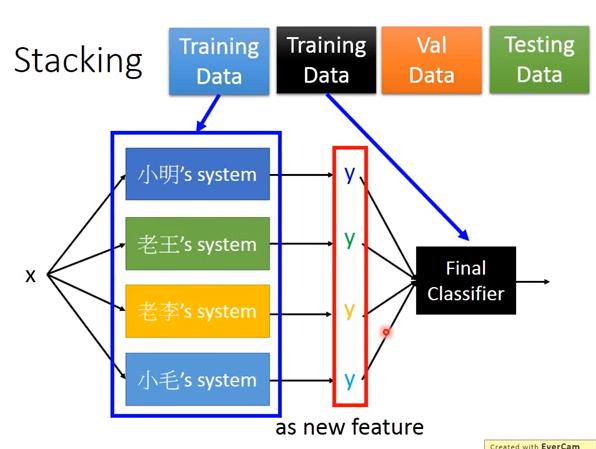
• 各個模型 和 final classifier 應該要用不同的 training data