Definition of VC Dimension
定義
假設最小的 break point 為k, 則最大的 non - break point 為 k-1, 即 VC Dimension
- 能夠 shatter 的最多 input
意義
假設 的 VC Dimension 為 N
- 可以 shatter 最多 N 個資料點
- 但不是任意 N 個資料點都能被 給 shatter
- 當 N 夠大, 也夠大時, 成長函數會比 N 的 VC dimension 次方來得小
- VC dimension 是 finite 的 Hypothesis set 才是好的
VC Dimension of Perceptrons
證明 PLA 在資料維度為 d 時, VC Dimension 是 d+1
- 證明 , 只要找到一種d+1筆的資料是可以被 PLA 給 shatter 的即可
證明 , 需要證明對於任何 d+2 筆的資料, PLA 都不能夠 shatter
本段證明看不懂
總之 PLA 的 VC Dimension 就是 d+1 ㄏㄏ
Physical Intuition of VC Dimension

- 和 M 一樣, VC Dimension 不論太大或太小都不好, 因此要選擇一個好的 VC Dimension
Interpreting VC Dimension
 假設壞事情( 和 差很多) 發生的機率為 , 則此時 generalization error , 等同於我們有 的信心水準使得 會落在 內
假設壞事情( 和 差很多) 發生的機率為 , 則此時 generalization error , 等同於我們有 的信心水準使得 會落在 內
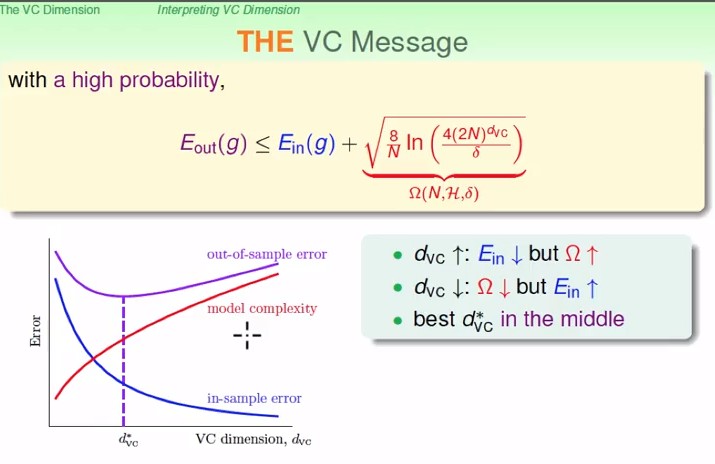
- 我們現在知道
- 這裡的 也就是我們付出的penalty, 而這個penalty會隨著 model的強大(VC Dimension的提高)而變得更大

- VC Dimension 可以說是 model 的 complexity