Youtube

Proximal Policy Optimization (PPO) 是 OpenAI 預設的 RL Algorithm

On-Policy -> Off-Policy

之前提到的 Policy Gradient 是 On-Policy 的做法，那為何需要 Off-Policy 呢?

• On-Policy 的做法每次更新 $\theta$ 就要重新 sample 一次資料，因此訓練的時間大量消耗在 sampling 上，非常耗時。
• Off-Policy 希望可以用 $\pi_{\theta'}$ 來蒐集 data，用這些 data 來訓練 $\theta$，就可以用相同的 data 來 update 很多次 $\theta$。

以下先介紹 importance sampling

Importance Sampling

從 p 這個 distribution 得到 x，要如何近似 f(x) 的期望值?

• $E_{x\sim p}[f(x)] \approx \frac{1}{N}\sum_{i=1}^N f(x^i)$
  • 這個作法是我們有辦法從 p 這個 distribution 裡 sample 出 x 時的作法，實際情況我們無法直接 sample，只能從 q 這個 distribution 做 sampling，原因稍後會說明

從 q 這個 distribution 去 sample x 的作法

• $E_{x\sim p}[f(x)] = \int f(x)p(x)dx = \int f(x)\frac{p(x)}{q(x)}q(x)dx = E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$
• 此時理論上 q 可以是任何 distribution，唯一限制是 q(x) 機率為0 時，p(x) 機率必定為 0 即可使用 importance sampling 的技巧。

然而實際上 p 和 q 的 distribution 不能差太多，為什麼?

• 雖然 從 p 和 q sample 出來的方式 期望值會相同，但是 VAR 會不同 (不太懂 VAR 不同又怎樣)
• 這段沒很懂，之後再重看

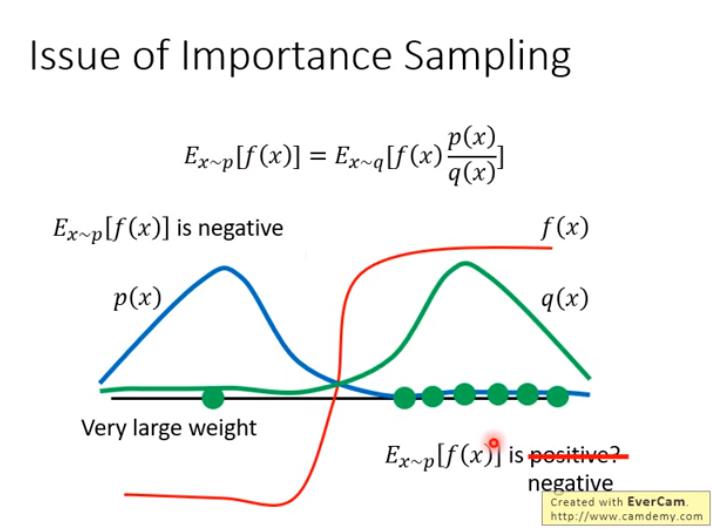以上圖為例：

• 若 p 和 q 差很多，sampling 的時候，可能只 sample 到 q(x) 機率很大的 x (然而 p(x) 很小)，而導致認為 $E_{x\sim p}[f(x)]$ 會是正的
• 解決的方法：
  1. sample 夠多的點，才能真正近似
  2. 讓 p 和 q 不要差太多

On-policy -> Off-policy (with Importance Sampling)

用 $\theta'$ 做示範(和環境互動)，讓 $\theta$ 學習

• 根據 importance sampling，$\nabla \bar {R_\theta} = E_{\tau\sim p_\theta (\pi)}[R(\tau)\nabla logp_\theta(\tau)] = E_{\tau\sim p_{\theta'} (\pi)}[\frac{p_\theta(\tau)}{p_{\theta'}(\tau)}R(\tau)\nabla logp_\theta(\tau)]$

老師表示：為了方便說明，在數學的部分做了大量簡化，這裡的講法並不嚴謹

• 本來應該使用 $A^\theta(s_t,a_t)$，這裡使用 $A^{\theta'}(s_t,a_t)$ 做近似
• 這裡也假設 $p_\theta(s_t)$ 和 $p_{\theta'}(s_t)$ 是幾乎相同的
• 最終得到 以 $\theta'$ 做 demonstration，來更新 $\theta$ 的 gradient $J^{\theta'}(\theta) = E_{(s_t,a_t)\sim \pi_{\theta'}}[\frac{p_\theta(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t,a_t)]$

Review: 從 On-policy 改成 Off-policy 是使用 importance sampling 的技巧，因此若 $p_\theta$ 和 $p_{\theta'}$ 差太多的話這招實務上就不奏效，那該如何避免它們差太多?

PPO / TRPO

• PPO 的前身是 TRPO，效果差不多，PPO較易實作
• 我覺得這個方程式的減號應該是加號? 要複習一下 KL divergence 了 $J_{PPO}^{\theta'}(\theta) = J^{\theta'}(\theta) - \beta KL(\theta,\theta')$
  • $KL(\theta,\theta')$ 量測的分布其實是指 $p_\theta(a_t|s_t)$ 和 $p_{\theta'}(a_t|s_t)$

PPO algorithm

• 和 policy gradient 不同的地方是，本來每個 iteration 只能更新一次 $\theta$，現在可以更新很多次

PPO2

• 這個方法非常好 implement

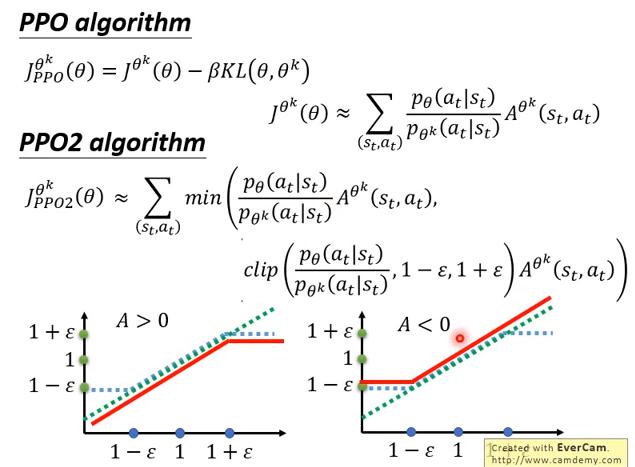
簡寫 $J \approx \sum min(\frac{p_\theta}{p_{\theta^k}}A^{\theta^k},clip(\frac{p_\theta}{p_{\theta^k}},1-\epsilon,1+\epsilon)A^{\theta^k})$

• 橫軸是 $\frac{p_\theta}{p_{\theta^k}}$，縱軸是 (決定A的係數的?)輸出
• 綠線：$\frac{p_\theta}{p_{\theta^k}}$ (identity function)
• 藍線：$clip(\frac{p_\theta}{p_{\theta^k}},1-\epsilon,1+\epsilon)$
  • $\epsilon$ 是一個可以調整的 hyperparameter (設0.1、0.2之類)

當 A大於0 時，取 min 後的輸出會是左圖的紅線；A小於0 時，取 min 後的輸出會是右圖的紅線，而這也很直觀，因為我們不希望 $p_\theta$ 和 $p_{\theta^k}$ 差太多，因此在 A大於0 時，雖然希望他調高 $p_\theta(a_t|s_t)$ 的機率，但又不希望他調高太多；反之 A小於0 時亦然。