Restriction of Break Point

在最小 Break Point $K = 2$ , 資料數量 $N = 3$ 的情況下
(在二元分類問題中) 若Hypothesis不能shatter任意兩筆資料, 結果會是Hypothesis set中最多只能有4個hypothesis。過程見影片較詳細。

Bounding Function: Basic cases

Bounding Function $B(N,k)$ : 最小的 Breaking Point 是 k, 在N筆資料時最多會有多少種dichotomy, 即成長函數的上界。

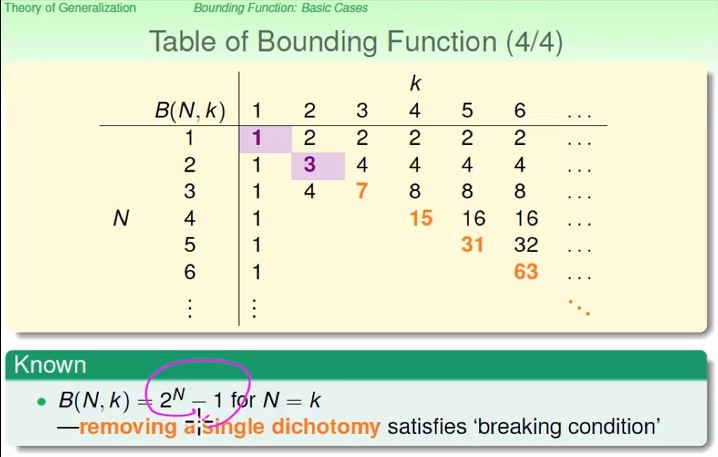
• 在 N < k 時, $B(N,k) = 2^N$
• 在 N = k 時, $B(N,k) = 2^N-1$

Bounding Function: Inductive Cases

經過一番證明(影片中較詳細), 我們可以知道Bounding Function的上限, 即表中任一數值的上限為其上方和左上方數值之和。

最後我們可以得到 $B(N,k) = \leq \sum\limits_{i=0}^{k-1}C_i^N$, 這會是一個N的多項式

A Pictorial Proof

但是我們想把 $E_{out}$ 變成有限的, 所以抽另外一組資料 $D'$ 來計算 ${E_{in}}'$ 當作 $E_{out}$

若使用各種DataSet來計算各種 $E_{in}$ 和 ${E_{in}}'$ 則這些 $E$ 的分布會如上圖右, 那麼在壞事情($E_{in}$ 和 $E_{out}$ 離很遠)發生的時候, $E_{in}$ 和 ${E_{in}}'$ 有超過1/2的機率也會離很遠。

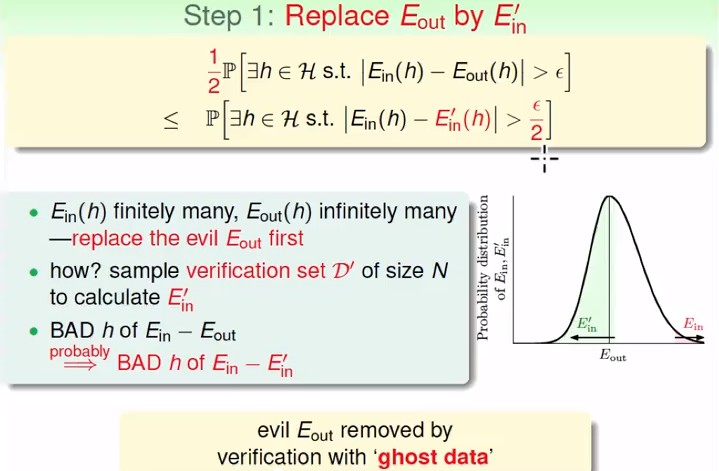
• $\frac{1}{2}P[\exists h \in H\ s.t.|E_{in}(h)-E_{out}(h)|>\epsilon]$: 1/2 * 壞事情發生的機率
• $P[\exists h \in H\ s.t.|E_{in}(h)-{E_{in}}'(h)|>\epsilon]$: $E_{in}$ 和 $E_{out}$ 離很遠的機率(改了標準)
• 即 $P[\exists h \in H\ s.t.|E_{in}(h)-E_{out}(h)|>\epsilon] \leq 2P[\exists h \in H\ s.t.|E_{in}(h)-{E_{in}}'(h)|>\epsilon]$

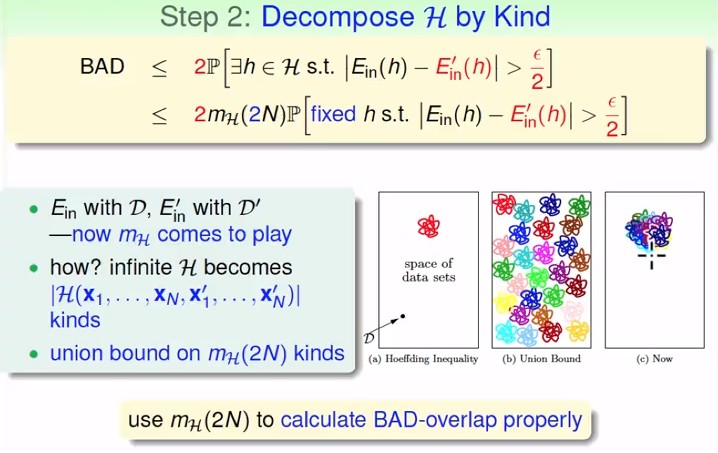
D有 $x_1$ 到 $x_N$, D' 有 ${x_1}'$ 到 ${x_N}'$, 我們本來有無限的$H$, 而現在只需要計算 $H(x_1,...,x_N,{x_1}',...,{x_N}')$ 可以分出多少種dichotomy, 即 $m_H(2N)$

• $|E_{in}-{E_{in}}'|$ : $E_{in}$ 跟 ${E_{in}}'$ 的差別
• $|E_{in}-\frac{E_{in}+{E_{in}}'}{2}|$ : $E_{in}$ 跟所有人的差別

所以用 $\epsilon /4$ 代入Hoeffding

Vapnik-Chervonenkis (VC) bound

從最後題目可以發現這個bound並不是這麼準, 下堂課會探討為啥明明不準還要推導這個bound, 還有要如何利用break point。