Perceptron Hypothesis Set

Perceptron

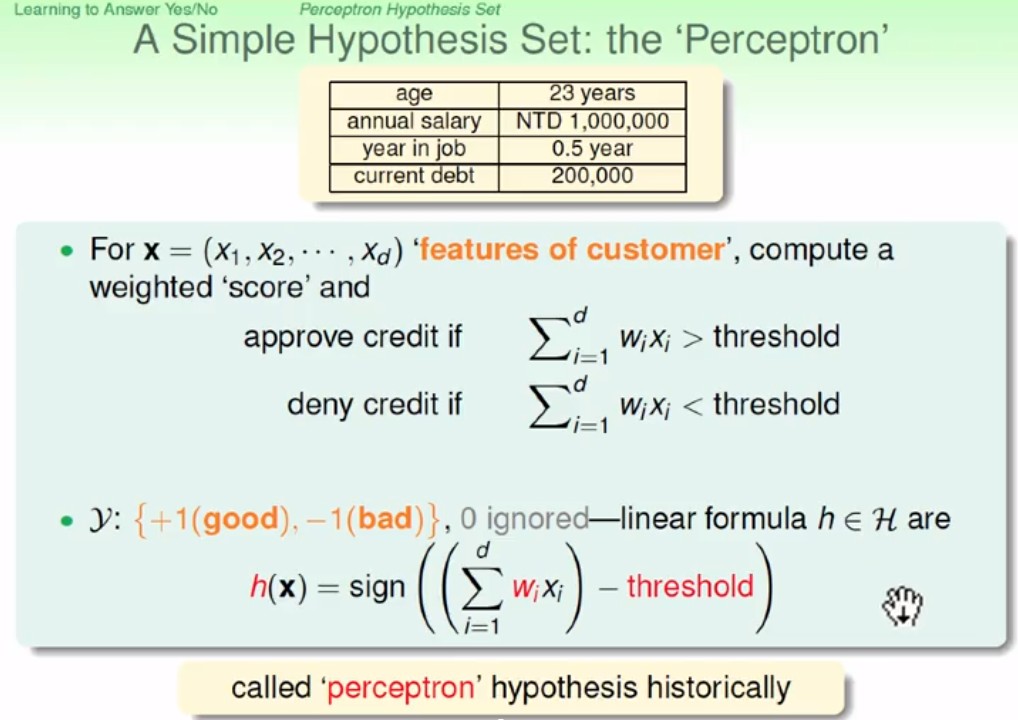找出各個$x_i$的權重$w_i$, 並判斷$\sum\limits_{i=1}^{d}w_ix_i$是否大於threshold(門檻), 是則輸出1, 否則輸出0

• $sign()$: 判斷正負號, 大於0則輸出1, 小於0則輸出-1

• 可以將 $h(x) = \sum\limits_{i=1}^{d}w_ix_i - \mathrm {threshold}$ 表示為 $h(x) = \sum\limits_{i=1}^{d}w_ix_i + w_0x_0=\sum\limits_{i=0}^{d}w_ix_i$ , $w_0$值為(-threshold), $x_0$值為1

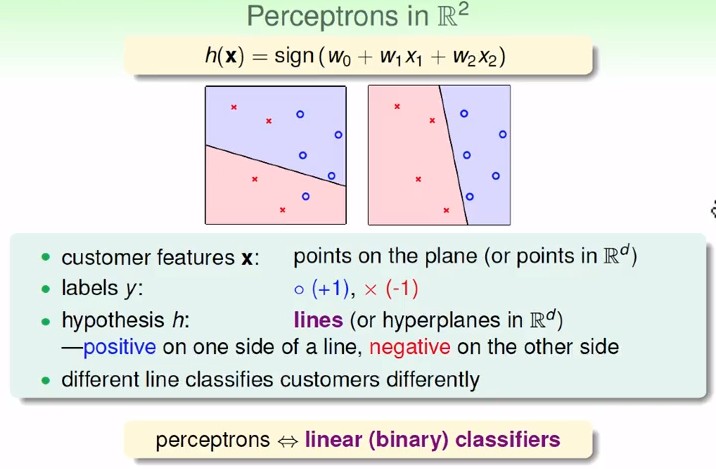
• perceptrons 又可稱線性分類器

Perceptron Learning Algorithm (PLA)

PLA如何逐步修正直線

當實際的結果(y)是正的，它(wx)跟我說負的，代表這個w跟x的角度夾角太大，修正的方式就是把它轉回來，把w跟x加起來成為新的w，那麼結果可能就會是正的，另外一種可能性，實際結果(y)是負的，結果它(wx)跟我說是正的，那代表w跟x的角度太小了 我就把w減掉x

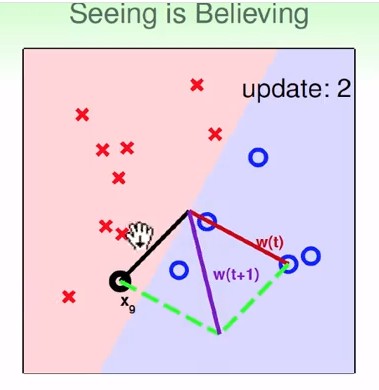
• PLA的進行 看影片較清楚
• 注意: w在圖中為分界線的法向量

Ans: 3 將 $w_{t+1} = w_t + y_nx_n$ 等號兩邊乘上 $y_nx_n$ 即可得知3正確

Guarantee of PLA

• $w_f$: 我們想要的那個未知的w
• ${w_f}^Tx_n$: $w_f$那條線與$x_n$點的距離(不知道為啥)
• $min_n(y_n{w_t}^Tx_n)$: 離線最近的點距離乘上y
• $x_{n(t)}$, $y_{n(t)}$: 第t次算出w犯錯的那個點的x和y
• 向量內積越大通常代表兩個向量越接近, 即 ${w_{t+1}}$ 比 $w_t$ 更接近 $w_f$
• 但是 ${w_f}^Tw_{t+1} > {w_f}^Tw_t$ 也有可能單純是因為 $w_{t+1}$ 的長度比 $w_t$ 更長, 導致我們以為${w_{t+1}}$ 比 $w_t$ 更接近 $w_f$

• 這裡證明了 $||w_{t+1}||^2 \leq ||w_t||^2$ , 也因此我們可以確定 ${w_{t+1}}$ 比 $w_t$ 更接近 $w_f$

最後那個問題不會解 ˊˋ

Non-Separable Data

Pocket Algorithm

• 在PLA過程中, 把最好的weight(犯最少錯誤)存著(在pocket中), 比較當前weight的表現