Neural Network Overview

Neural Network Representation

Computing a Neural Network's output

以矩陣表示Neural Network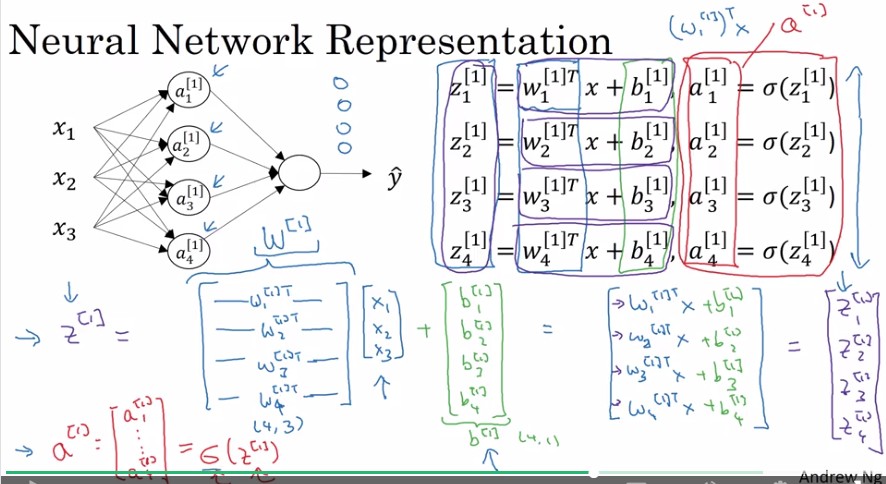

• a(或z)向量(column vector) 可以表示一層hidden layer

Vectorize across multiple examples

• $x^{(n)}$: 第n筆 training data
• $z^{[i](j)}$: hidden layer 第 i 層, 第 j 筆 training data (嗎

maybe

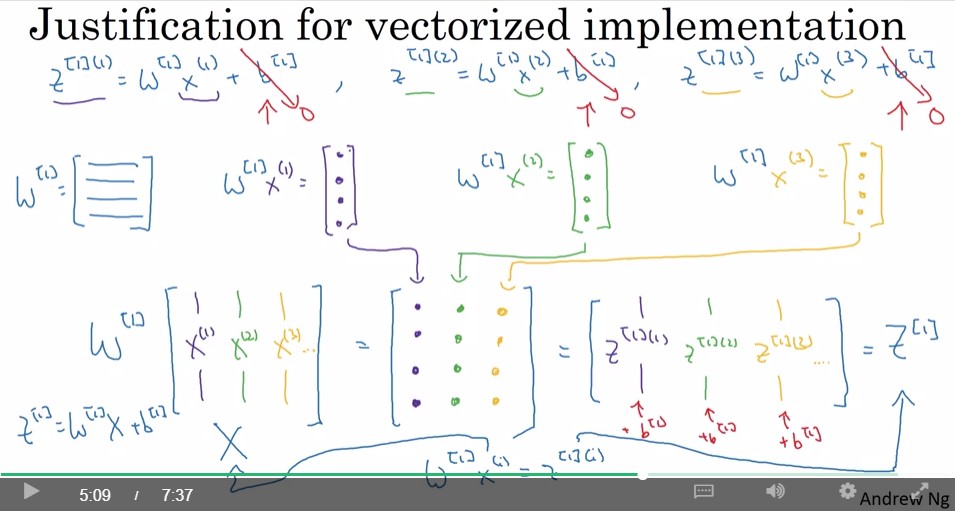
Explanation for Vectorized implementation

Activation Functions

tanh函數(Hyperbolic tangent function): 平均值為0, 比sigmoid好?
希望output為0~1時, 使用sigmoid function
希望output為-1~1時, 使用tanh function

tanh和sigmoid 的共同缺點: 當z很大或很小時, gradient descent效率很差

Rectified Linear Unit (ReLU)
Leaky ReLU

Why do you need non-linear activation functions?

沒看影片 參考

• 神经网络激励函数的作用是什么？有没有形象的解释？(後段含sigmoid, tanh 和 ReLU的比較)
• 莫烦Python - 激励函数(Activation Function)

Derivatives of activation functions

介紹 sigmoid, tanh, ReLU, Leaky ReLU 的微分

Gradient Descent for neural networks

(以單層hidden layer的neural network而言)參數:

• $w^{[1]}, b^{[1]}$: hidden layer的權重&常數向量
• $w^{[2]}, b^{[2]}$: output layer的權重&常數向量
• $n^{[0]}$: 即nx, input feature的數量
• $n^{[1]}$: hidden layer 的 unit數量
• $n^{[2]}$: (不計input layer的)第二層 unit 數量, 在此為output layer, 所以值為1

Cost Function:
$J(w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}) = \frac{1}{m}\sum\limits_{i=1}^m h(\hat y,y)$

Gradient Descent:
Repaeat{

• ???
• $dw^{[1]} = \frac{\partial J}{\partial w^{[1]}}, db^{[1]} = \frac{\partial J}{\partial b^{[1]}},$ ...
• $w^{[1]} = w^{[1]} - \alpha dw^{[1]}$
• $b^{[1]} = b^{[1]} - \alpha db^{[1]}$
• ???

}

Forward propagation & Back propagation

• keepdims = True 會把輸出的維度從rank-1陣列(n, )變成符合輸入矩陣維度(這個例子是二維)的matrix

Random initialization

為什麼參數要隨機初始化, 不全初始為0就好?

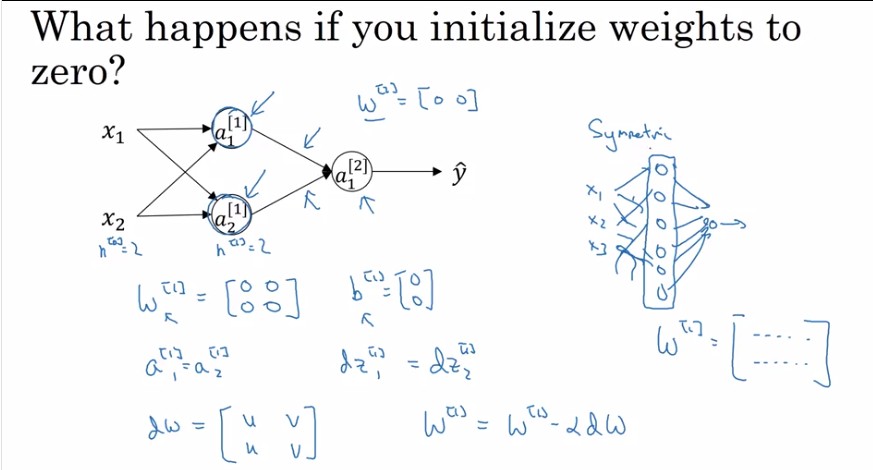
• 若把所有參數都初始化為0, 則所有hidden units都會計算相同的function, 我們要的是各個hidden units做不同的事, 所以才需要random initialization

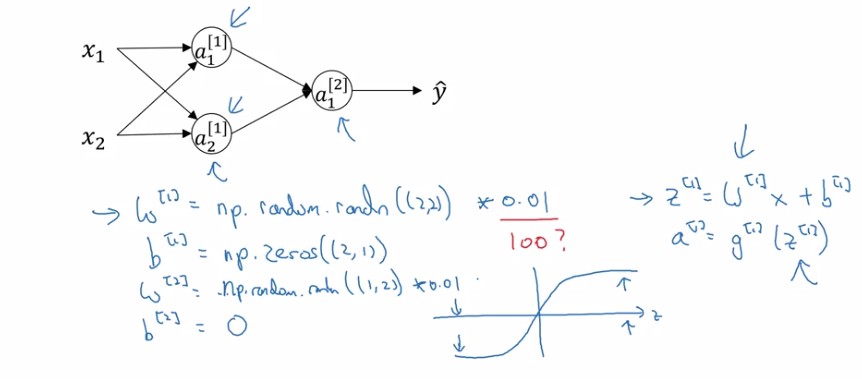
• b可以都初始化為0, 因為將w初始化為random之後, 每個hidden unit已經是在計算不同的function了。
• 將random後的w再乘上0.01而不是乘上較大的數字, 是因為若乘上大數, 則z值會很大, sigmoid這種function的圖形會在z值很大的時候有很小的微分, 導致gradient descent學習速率很慢。