Computer Vision
Edge Detection Example
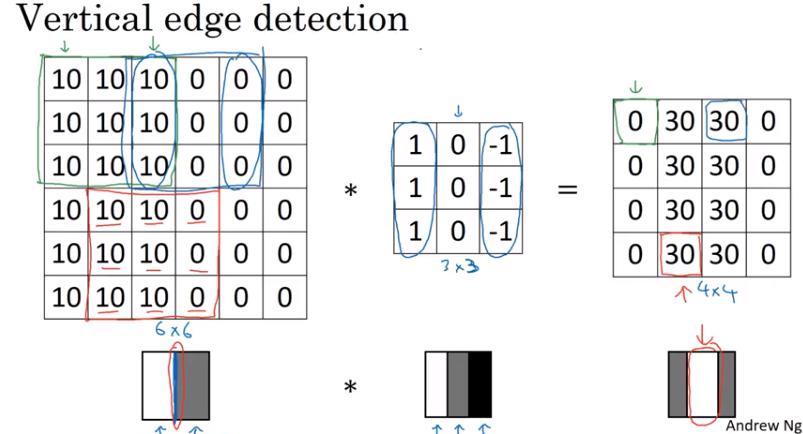
More Edge Detection
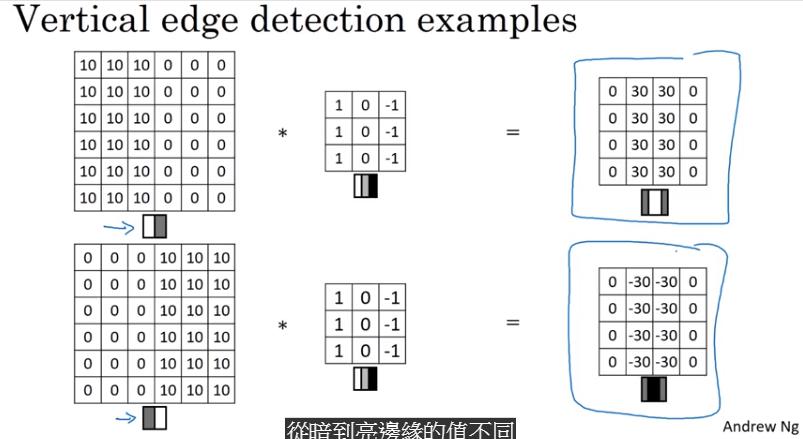
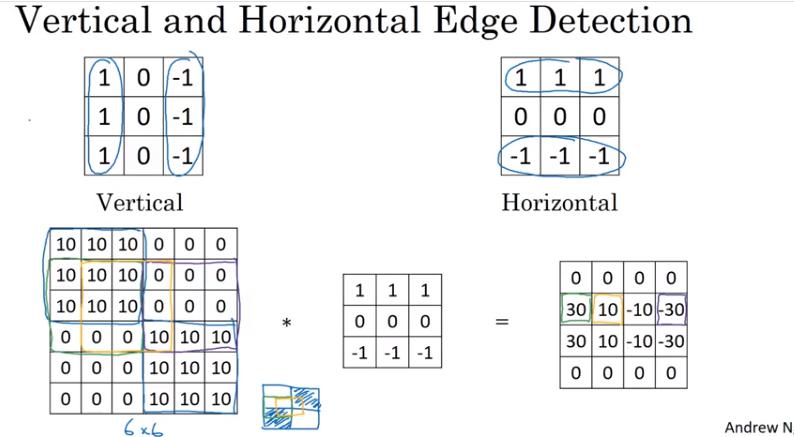
- 這個 example 是水平的 filter
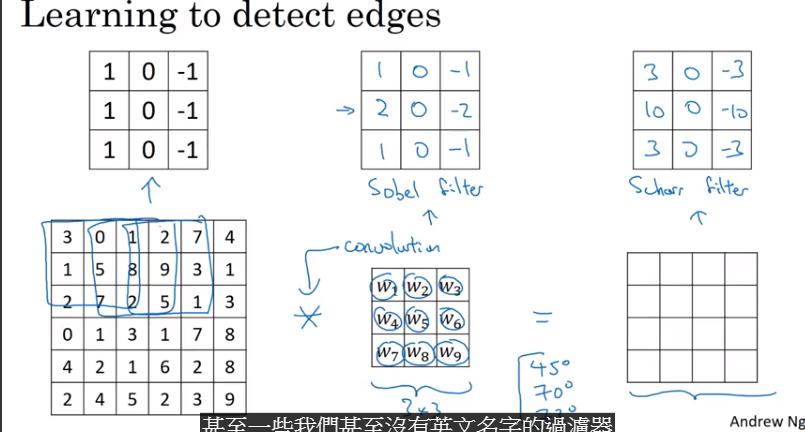
- sobel: 中間的權重更多,可以更 robust
Padding
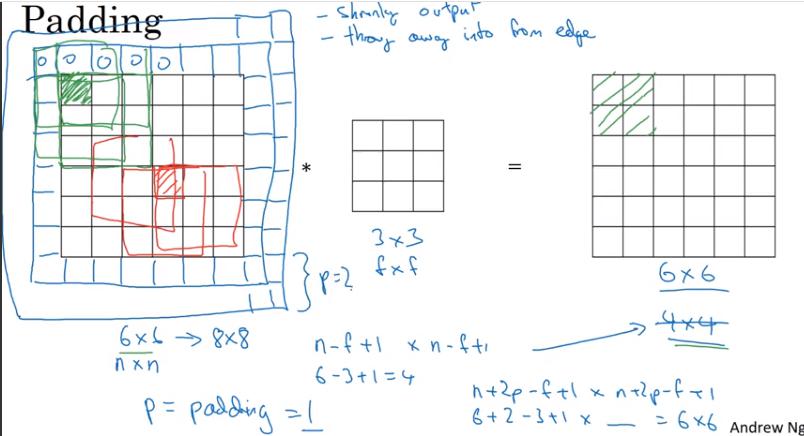
- 沒有 padding 的壞處:
- 每經過一層,output 的圖片就越來越小,有時不希望這樣,例如想做非常深的 network
- 角落的 pixel 只會計算到一次 convolution;而圖片中間的 pixel 可以被計算到很多次,導致丟棄許多邊緣的影像資訊
Valid Convolution: 不做 padding
- 原 output size: n-f+1 * n-f+1
Same Convolution: padding 使得 output 和 input size相同
- padding 之後的 output size: n+2p-f+1 * n+2p-f+1
- 解 n+2p-f+1 = n, 得 p = (f-1)/2
filter size 通常是奇數,ex: 3x3、5x5、7x7、1x1
- 這樣 same convolution 的 padding 就可以直接對稱
- 維度是奇數的 filter 會有一個中心點,可以記為它的位置,較恰當
Strided Convolutions
stride = 2 時,不論行 or 列 都跳 2 步
- 圖片大小:
- filter 大小:
- padding:
- stride:
輸出大小:
如果不是整數則無條件捨去,也就是 filter 超出圖片就不計算 conv 輸出大小:
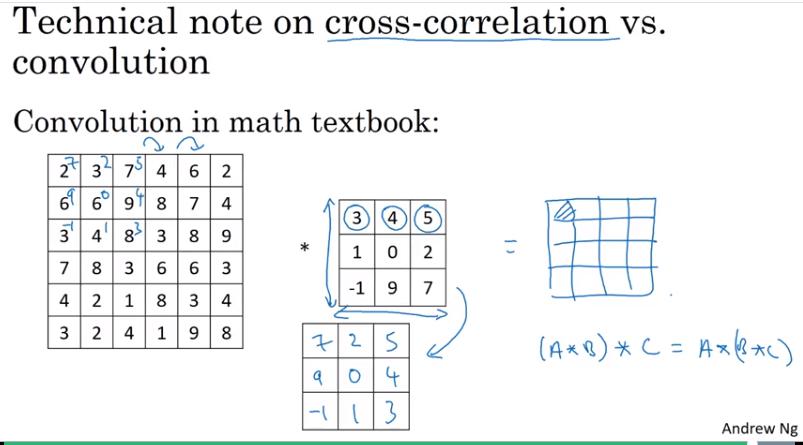
Convolutions Over Volume
- input:
- filter:
- ex: 的 filter 就有 27 個參數 (後面會提到其實還要加 bias,也就是其實有 個參數。有幾個 filter 就有幾個 bias)
- output: ,只有 2 個維度
- 然而 filter 會有很多個,因此實際 output size 是
input 和 filter 的 應該要一樣 (也有人稱 depth,但較容易 confusing) output 的 channel 數就是這層 filter 的個數
One Layer of a Convolutional Network
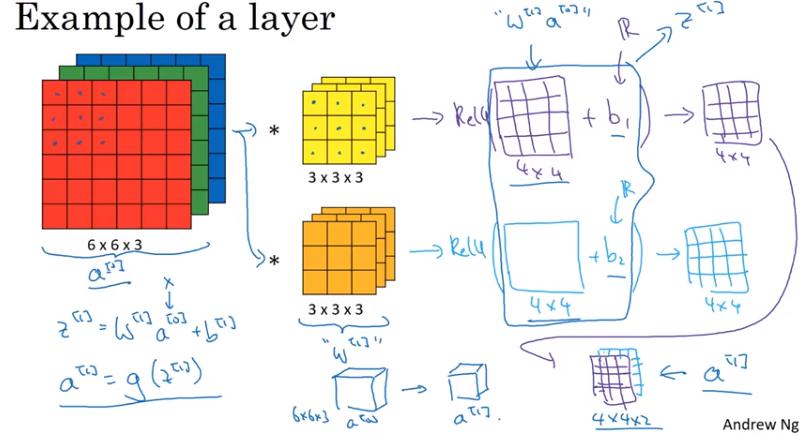
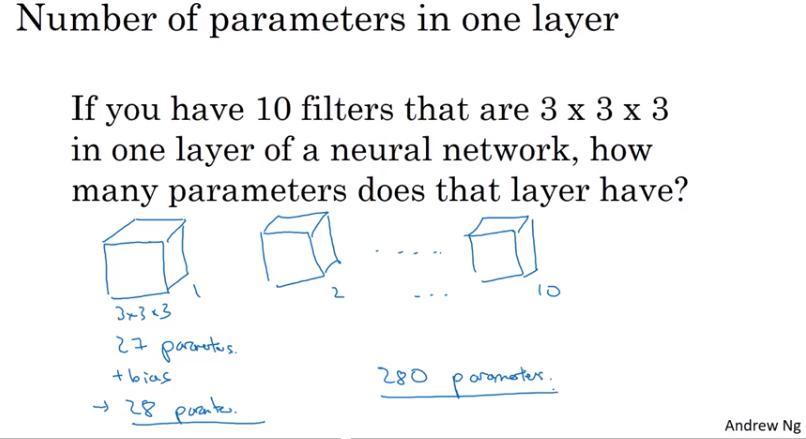
- 這樣做有個好處:不論 input 的圖片有多大,參數量都是固定的

Simple Convolutional Network Example

Pooling Layers
Hyperparamters
- filter size
- stride
常見的 pooling layer 設定
- filter size = 2,stride = 2
- 使得 output 長寬都縮為一半
- 很少做 padding
Output Size
- Convolutional Layer 的 output size 公式同樣適用於 pooling layer
- 其中一邊的 output:
- pooling 會在不同 channel 各自獨立計算,即 output 的 channel 數會等於上一層 output 的 channel 數
Max Pooling Intuition
直觀而言,若在圖片的任何地方偵測到該 feature,就在該區域保持最大值
Average Pooling
很少人使用
例外情況:NN 非常 deep 的時候,會使用 Average Pooling 來壓縮,例如將 7x7x1000 的 feature map 壓縮成 1x1x1000
另外補充:
- Global Average Pooling 是把整個 feature map 做平均,得到一個值,有幾個 feature map 就 output 幾個值
- 本質上跟一般的 pooling 一樣,只是 filter size 變成整個 feature map 的 size
Pooling layers have NO parameters to learn
CNN Example
非常類似 LeNet-5 的 example
- 計算 layer 數時,有的文獻將 conv+pooling 視為同一層,有的視為兩層。通常以需要訓練的 (有權重的) 才算一層較為恰當,因此本影片將 conv+pooling 視為同一層。
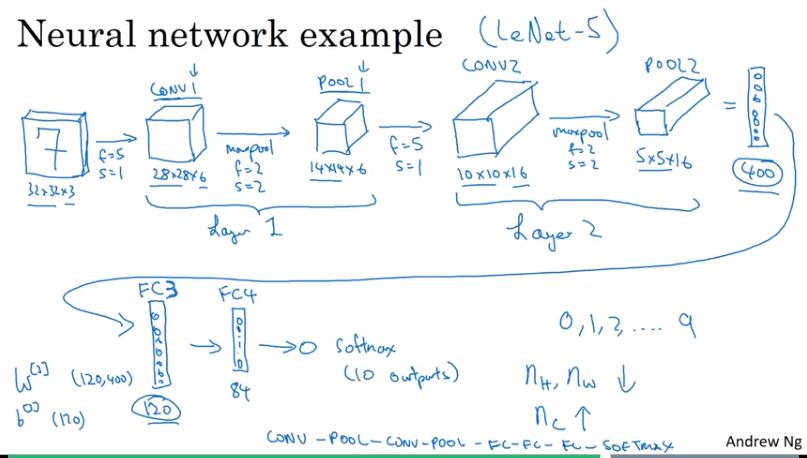
- 方塊是指該層的 output size
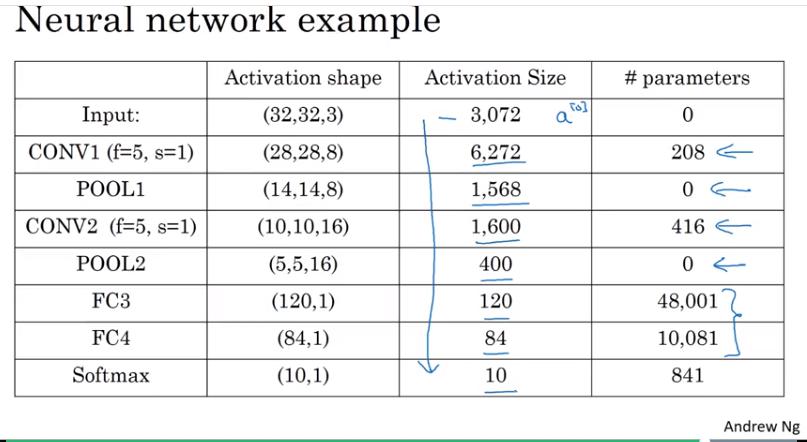
- 架構較深時,activation size (output size) 下降太快的話沒什麼幫助
Why Convolutions?
- 參數共享
- 稀疏連接